策略梯度

参考：B站视频

基础概念

经验轨迹$τ$

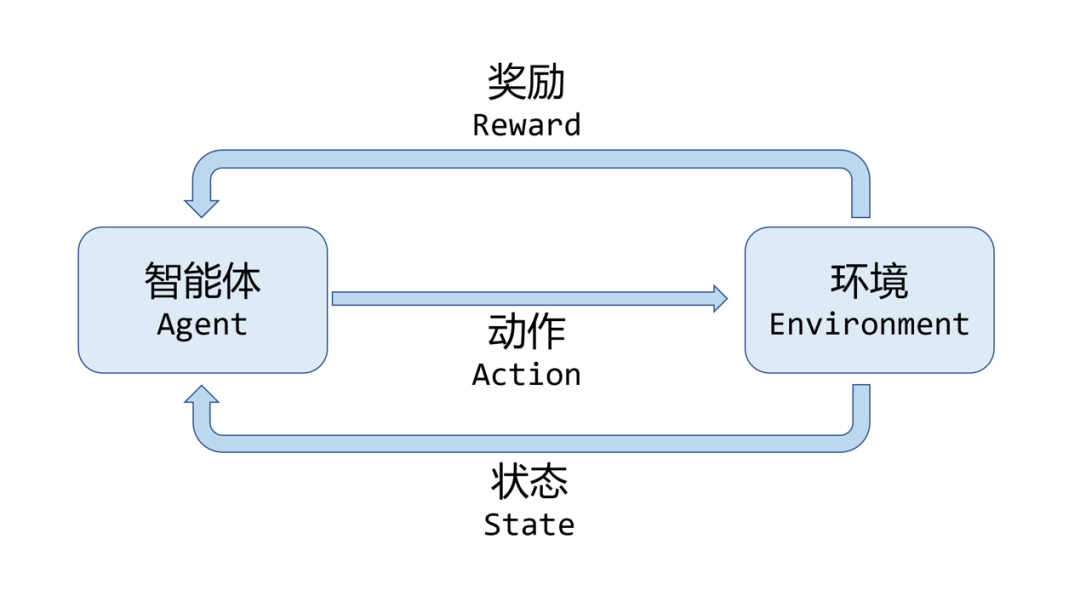
南大本科生论文获NeurIPS Poster！俞扬团队首次揭示强化学习「记忆池」最优利用方法|记忆|俞扬|南大_新浪新闻

智能体可以感知到当前的环境状态，然后作出行为，会影响环境的状态并从环境中得到奖励。这里将状态表示为$s$，智能体的行为表示为$a$，智能体得到的奖励为$r$。

那么智能体与环境交互一次的经验轨迹为 $ \tau = s_0, a_0, r_1, s_1, \cdots, a_{T - 1}, r_T, s_T $，其中 $ T $ 为终止时刻。就是状态、智能体采取的动作、智能体得到的奖励、下一状态……的一个数列。

经验轨迹的概率 $ P_\theta(\tau) $

经验轨迹出现的概率由环境和智能体两部分决定：

$\begin{align*} P_\theta(\tau) &= p(s_0) \cdot \pi_\theta(a_0 \mid s_0) \cdot p(s_1 \mid s_0, a_0) \cdot \pi_\theta(a_1 \mid s_1) \cdots \pi_\theta(a_{T - 1} \mid s_{T - 1}) \cdot p(s_T \mid s_{T - 1}, a_{T - 1}) \\ &= p(s_0) \prod_{i = 0}^{T - 1} \pi_\theta(a_i \mid s_i) \cdot p(s_{i + 1} \mid s_i, a_i) \end{align*}$

在这里，$p(s_0)$ 代表的是初始状态$s_0$出现的概率，$ \pi_\theta(a_0 \mid s_0) $代表的是在初始状态初始状态$s_0$下Agent选择行为$a_0$的概率（跟策略$\pi$有关），$p(s_1 \mid s_0, a_0)$代表着在Agent选择动作$a_0$和$s_0$的状态下，转移到$s_1$的概率。

其中，策略$\pi$受参数$\theta$影响，$ p(s_0) $ 和 $ p(s’ \mid s, a) $ 由环境决定，与 $ \theta $ 无关。

经验轨迹出现的概率与$\theta$有关的就只有$ \pi_\theta(a_0 \mid s_0) $。

累积回报 $ R(\tau) $

每一次行动，智能体都会得到一个奖励，将这次行动$r_1\cdots r_T$所有的奖励加起来就能得到累计回报。其是经验轨迹的函数，因为策略一个经验轨迹可以计算出一个累计回报。

$R(\tau) = r_1 + r_2 + \cdots + r_{T - 1} + r_T = \sum_{t = 1}^T r_t$

累积期望回报 $ \bar{R}_\theta $

真实的累积回报为采样得到累积回报的期望，即：

$\bar{R}_\theta = E_{\tau \sim P_\theta(\tau)}[R_\tau] = \sum_\tau R(\tau)P_\theta(\tau)$

在选定一个策略$\pi$的情况下（也就是选择参数$\theta$的情况下），可以得到每一个策略轨迹$\tau$出现的概率和通过策略轨迹$\tau$得到的累计回报。所以将所有的策略轨迹加权求和，就可以得到在策略$\pi$的情况下的一个累计期望回报 $ \bar{R}_\theta $。

算法

策略梯度的想法是，找到一个策略$\pi$使得能得到的累积期望回报最大。

$\arg\max_{\theta} \bar{R}_\theta$

而又因为 $ \bar{R}_\theta $是$\theta$的函数，所以可以通过求导的方式找到$\theta$使得 $ \bar{R}_\theta $最大。所以首先要对其求梯度。

对 $ \bar{R}_\theta $ 关于 $ \theta $ 求梯度：

$\nabla \bar{R}_\theta = \sum_\tau R(\tau) \nabla P_\theta(\tau) = \sum_\tau R(\tau) P_\theta(\tau) \frac{\nabla P_\theta(\tau)}{P_\theta(\tau)}$

因为$R(\tau) $跟策略是无关的，给定了经验轨迹就能计算出一个累计回报。

由于

$\nabla \log y = \frac{\nabla y}{y}$

那么

$\nabla \bar{R}_\theta = \sum_\tau R(\tau)P_\theta(\tau)\nabla \log P_\theta(\tau) = E_{\tau \sim P_\theta(\tau)}[R(\tau)\nabla \log P_\theta(\tau)]$

因为转为$\log$之后可以将$P_\theta(\tau)$中的乘法拆为加法。

上面期望符号可以通过采样消除，即 $N$ 次采样后，得到

$\nabla \bar{R}_\theta = \frac{1}{N} \sum_{n=1}^N R(\tau^n)\nabla \log P_\theta(\tau^n)$

因为真实的经验轨迹的概率分布是未知的，所以只能靠多次采样来近似期望。

对 $P_\theta(\tau)$ 求对数，得到

$\begin{align*} \log P_\theta(\tau) &= \log p(s_0) + \log \pi_\theta(a_0 \mid s_0) + \log p(s_1 \mid s_0,a_0) + \log \pi_\theta(a_1 \mid s_1) + \cdots + \log \pi_\theta(a_{T - 1} \mid s_{T - 1}) + \log p(s_T \mid s_{T - 1},a_{T - 1}) \\ &= \log p(s_0) + \sum_{t = 0}^{T - 1} [\log \pi_\theta(a_t \mid s_t) + \log p(s_{t + 1} \mid s_t,a_t)] \end{align*}$

对 $\log P_\theta(\tau)$ 关于 $\theta$ 求梯度，由于 $p(s’ \mid s,a)$ 与 $\theta$ 无关，因此全部被消掉，得到

$\nabla \log P_\theta(\tau) = \sum_{t = 0}^{T - 1} \nabla \log \pi_\theta(a_t \mid s_t)$

将 $\nabla \log P_\theta(\tau)$ 代入 $\nabla \bar{R}_\theta$，得到策略梯度：

$\nabla \bar{R}_\theta = \frac{1}{N} \sum_{n = 1}^N R(\tau^n) \sum_{t = 0}^{T - 1} \nabla \log \pi_\theta(a_t^n \mid s_t^n) = \frac{1}{N} \sum_{n = 1}^N \sum_{t = 0}^{T - 1} R(\tau^n)\nabla \log \pi_\theta(a_t^n \mid s_t^n)$

然后用$\theta+\eta\nabla \bar{R}_\theta $就可以优化$\theta$使得累积期望回报越来越高。其中$\eta $是学习率。

总结一下，就是通过多次采样，得到多条经验轨迹，然后将每条经验轨迹得到的累计奖励做加权求和，从而得到平均累计奖励。通过梯度上升的方式，对$\theta$求导，得到平均累计奖励最大的时候的$\theta$。

TRPO

全称叫Trusted Region Policy Optimization。

参考：基本思想、算法讲解、公式推导、手写推导

这里的公式真是太复杂了TvT

思想

普通的策略梯度有一个问题，就是采样导致的随机性太强了。当步长不合适时，更新的参数所对应的策略是一个更不好的策略，当利用这个更不好的策略进行采样学习时，再次更新的参数会更差，因此很容易导致越学越差，最后崩溃。

TRPO的思想是，当策略更新后，累积期望回报的值不能更差。这样TRPO就可以逐渐接近最优解。

基础概念

Trust Region

Trust Region就是TRPO的前两个词，中文为置信域。

它的想法是如果想要在$x \in X$中找到一个函数$f(x)$的最大值。而$f(x)$又不好求解，就可以在一个小邻域内，做$f(x)$的一个近似，在近似函数上找最大值。类似泰勒展开的思想。

形式化的表达如下，假设问题是：

$\text { Find } \boldsymbol{\theta}^{\star}=\underset{\boldsymbol{\theta}}{\operatorname{argmax}} J(\boldsymbol{\theta}) .$

要通过迭代找出最优的 $\boldsymbol{\theta}$ ，假设上一步迭代得到的解为 $\boldsymbol{\theta}_{\text{old}}$ 。那么设 $\mathcal{N}(\boldsymbol{\theta}_{\text{old}})$ 为 $\boldsymbol{\theta}_{\text{old}}$ 的一个邻域，例如： $\mathcal{N}(\boldsymbol{\theta}_{\text{old}})=\{\boldsymbol{\theta}||\boldsymbol{\theta}-\boldsymbol{\theta}_{\text{old}}|_{2} \leq \Delta\}$ 。若存在一个函数 $ L(\boldsymbol{\theta} \mid \boldsymbol{\theta}_{\text{old}})$ 能在 $\mathcal{N}(\boldsymbol{\theta}_{\text{old}})$ 内很好地近似 $J(\boldsymbol{\theta})$ ，则 $\mathcal{N}(\boldsymbol{\theta}_{\text{old}})$ 被称为Trust Region。

折扣回报函数

定义折扣回报函数 $\eta(\pi)$ 为：

$\eta(\pi)=\mathbb{E}_{s_{0}, a_{0}, \ldots}\left[\sum_{t=0}^{\infty} \gamma^{t} r\left(s_{t}\right)\right]$

其中$\gamma $是折扣因子。整条式子的意思是，一条经验轨迹是从$t=0$时刻到$t=\infty$，其中经过了一系列状态$s_0$到$s_\infty$，每个状态得到的奖励为$ r\left(s_{t}\right)$。因为未来的奖励相对及时奖励更没有吸引力，所以$t=0$的奖励没有折扣，而从$t=1$开始，就要给奖励乘上$t$个折扣因子$\gamma $。

所以回报函数 $\eta(\pi)$ 和累计回报其实是类似的，代表Agent能得到的奖励，只不过加上了折扣率。

优势函数

设$Q_{\pi}\left(s, a\right)$是在策略$\pi$，状态$s$下，选择动作$a$所能获得的奖励值。那就可以算出在策略$\pi$下，状态$s$的价值：

$V_{\pi}(s)=\pi\left(a_{1} \mid s\right) Q_{\pi}\left(s, a_{1}\right)+\cdots+\pi\left(a_{n} \mid s\right) Q_{\pi}\left(s, a_{n}\right)$

定义$A_{\pi}(s, a)=Q_{\pi}(s, a)-V_{\pi}(s)$为优势函数。因为$\pi\left(a_{i} \mid s\right)$是在状态$s$下选择动作$a$的概率，所以$V_{\pi}(s)$等于$Q_{\pi}\left(s, a_i\right)$的加权均值。如果$A_{\pi}(s, a)$大于0，则说明选择动作$a$，得到的价值比平均值更大。

重要性采样

参考文章

其的想法是当想求$X$关于某一个函数$f(x)$的期望时，即求$E=\mathbb{E}_{x \sim p(x)}[f(x)]$。如果随机变量 $X$ 无法直接从原始分布 $p(x)$ 下采样，那么可以另辟蹊径，从一个简单，可采样，定义域与 $p(x)$ 相同的概率分布 $\tilde{p}(x)$中进行采样。由于最终目标是求 $E = \mathbb{E}_{x \sim p(x)}[f(x)]$，那么可以进行简单的推导：

$\begin{aligned} E & =\mathbb{E}_{x \sim p(x)}[f(x)] \\ & =\int_{x} p(x) f(x) d x \\ & =\int_{x} \tilde{p}(x) \frac{p(x)}{\tilde{p}(x)} f(x) d x \\ & =\mathbb{E}_{x \sim \tilde{p}(x)}\left[\frac{p(x)}{\tilde{p}(x)} f(x)\right] \end{aligned}$

此时可以发现，原始问题转化成了求概率分布 $\tilde{p}(x)$ 下 $\frac{p(x)}{\tilde{p}(x)} f(x)$ 的期望，而此时概率分布 $\tilde{p}(x)$ 是我们寻找的一个简单，可采样的分布，且 $p(x), f(x)$ 都可以将样本 $x$ 输入到 $p$ 和 $f$ 中得到。那么依然可以通过蒙特卡洛法，从 $\tilde{p}(x)$ 中采样大量的样本来近似计算。

算法

网上看到的博客用了和刚才策略梯度的另一套符号，所以无奈下只能换了一套符号。

因为TRPO算法想累积期望回报的值不能更差，所以就希望新的$\eta(\tilde{\pi})$会比原先的$\eta(\pi)$更大。也就是希望$\eta(\tilde{\pi})-\eta(\pi)>0$。

所以就要知道$\eta(\tilde{\pi})-\eta(\pi)$的结果是什么，然后再更新策略的时候使之大于0即可。

针对这一想法，Sham Kakade于2002年提出了以下等式：

$\eta(\tilde{\pi})=\eta(\pi)+\mathbb{E}_{s_{0}, a_{0}, \cdots \sim \tilde{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t} A_{\pi}\left(s_{t}, a_{t}\right)\right]$

证明过程为：
$\begin{aligned} &\mathbb{E}_{\tau \mid \tilde{\pi}}\left[\sum_{t = 0}^{\infty} \gamma^{t} A_{\pi}\left(s_{t}, a_{t}\right)\right] \\ &= \mathbb{E}_{\tau \mid \tilde{\pi}}\left[\sum_{t = 0}^{\infty} \gamma^{t}\left(Q_{\pi}(s_t, a_t)-V_{\pi}\left(s_{t}\right)\right)\right] \quad \text{（优势函数定义）} \\ &= \mathbb{E}_{\tau \mid \tilde{\pi}}\left[\sum_{t = 0}^{\infty} \gamma^{t}\left(r\left(s_{t}\right)+\gamma V_{\pi}\left(s_{t + 1}\right)-V_{\pi}\left(s_{t}\right)\right)\right] \\ &= \mathbb{E}_{\tau \mid \tilde{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t}r(s_{t}) + \sum_{t=0}^{\infty}\gamma^{t+1}V_{\pi}(s_{t+1}) - \sum_{t=0}^{\infty}\gamma^{t}V_{\pi}(s_{t})\right] \quad \text{（线性性质拆分求和）} \\ &= \mathbb{E}_{\tau \mid \tilde{\pi}}\left[-V_{\pi}(s_{0}) + \sum_{t=0}^{\infty}\gamma^{t}r(s_{t})\right] \\ &= -\mathbb{E}_{\tau \mid \tilde{\pi}}\left[V_{\pi}(s_{0})\right] + \mathbb{E}_{\tau \mid \tilde{\pi}}\left[\sum_{t=0}^{\infty}\gamma^{t}r(s_{t})\right] \\ &= -\eta(\pi) + \eta(\tilde{\pi}) \end{aligned}$
其中：

$\sum_{t=0}^{\infty} \gamma^{t+1} V_{\pi}\left(s_{t+1}\right)-\sum_{t=0}^{\infty} \gamma^{t} V_{\pi}\left(s_{t}\right)$，因为前者的第1项就是后者的第2项，所以相减之后只保留了后者的第二项$-V_{\pi}\left(s_{0}\right)$。

$\sum_{t=0}^{\infty} \gamma^{t} r\left(s_{t}\right)$就是折扣回报函数的定义。就等价于$V_{\tilde\pi}\left(s_{0}\right)$，因为前面是在$\tilde\pi$策略下求期望。

$V_{\pi}\left(s_{0}\right)$的意思是$s_0$在$\pi$策略下的价值，也就是Agent能获得的价值，和折扣回报函数是一个意思！

可以将$\mathbb{E}_{s_{0}, a_{0}, \cdots \sim \tilde{\pi}}\left[\sum_{t=0}^{\infty} \gamma^{t} A_{\pi}\left(s_{t}, a_{t}\right)\right]$拆开，因为其代表的是不同的经验轨迹$\tau$下，采取策略$\tilde\pi$所能获得的所有经过折扣的优势函数的值的期望。所以：

$\begin{align*} \mathbb{E}_{s_0, a_0, \dots \sim \tilde{\pi}} \left[ \sum_{t=0}^{\infty} \gamma^t A_{\pi}(s_t, a_t) \right] &= \sum_{t=0}^{\infty} \gamma^t \mathbb{E}_{s_t, a_t\sim \tilde{\pi}} \left[ A_{\pi}(s_t, a_t) \right] \quad \text{（线性期望性质）} \\ &= \sum_{t=0}^{\infty} \gamma^t \sum_{s} P(s_t = s \mid \tilde{\pi}) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a) \quad \text{（状态-动作联合分布分解）} \\ &= \sum_{t=0}^{\infty} \sum_{s} \gamma^t P(s_t = s \mid \tilde{\pi}) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a) \quad \text{（交换求和顺序）} \end{align*}$

其中：

$\mathbb{E}_{s_{t}, a_{t} \sim \tilde{\pi}}\left[A_{\pi}\left(s_{t}, a_{t}\right)\right]$就是在$\tilde\pi$策略下，在$t$时刻，不同的$s_t,a_t$所能得到的均值。是一个联合分布，所以均值为：$\sum_{s} \sum_{a} P(s_t=s ,a\mid \tilde{\pi}) A_{\pi}(s, a)$，然后再拆成条件概率就可以得到$\sum_{s} P\left(s_{t}=s \mid \tilde{\pi}\right) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)$

由于 $P\left(s_{t}=s \mid \tilde{\pi}\right) \sum_{a} \tilde{\pi}(a \mid s) \gamma^{t} A_{\pi}(s, a) $是收敛的（有限MDP过程），因此两个求和符号可交换位置。

最终可以写成$\sum_{t=0}^{\infty} \sum_{s} \gamma^t P(s_t = s \mid \tilde{\pi}) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a) $

定义 $\rho_{\pi}$ 为：

$\rho_{\pi}(s)=P\left(s_{0}=s|\pi\right)+\gamma P\left(s_{1}=s|\pi\right)+\gamma^{2} P\left(s_{2}=s|\pi\right)+\ldots=\sum_{t = 0}^{\infty} \gamma^{t} P\left(s_{t}=s|\pi\right)$

就可以将上式进一步写成：

$\sum_{s} \rho_{\tilde{\pi}}(s) \sum_{a} \tilde{\pi}(a \mid s) A^{\pi}(s, a)$

所以$\eta(\tilde{\pi})=\eta(\pi)+\sum_{s} \rho_{\tilde{\pi}}(s) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)$

这里如果$\sum_{a} \tilde{\pi}(a \mid s) A^{\pi}(s, a)>0$的话，整个式子就是非负的，$\eta(\tilde{\pi})$也是非减的，但有时候可能因为噪声？导致$\sum_{a} \tilde{\pi}(a \mid s) A^{\pi}(s, a)<0$。所以也不是绝对递增的。这里我也没太搞清楚。

这时状态$s$的分布由新的策略产生，对新的策略严重依赖。也就是$\rho_{\tilde{\pi}}(s)$依赖新策略。这导致很难找到最大的$\sum_{s} \rho_{\tilde{\pi}}(s) \sum_{a} \tilde{\pi}(a \mid s) A^{\pi}(s, a)$。因为每个新策略都会导致$\rho_{\tilde{\pi}}(s)$不一样，所以就采取旧的策略$\rho_{\pi}(s)$所对应的状态分布代替$\rho_{\tilde{\pi}}(s)$。当新旧参数很接近时，用旧的状态分布代替新的状态分布是合理的。

这里就是Trust Region的应用，因为$\rho_{\tilde{\pi}}(s)$难求，所以在限制旧策略$\pi$和新策略$\tilde \pi$接近的情况下，用$\rho_{\pi}(s)$代替$\rho_{\tilde{\pi}}(s)$。这里作者用了KL散度来约束旧策略$\pi$和新策略$\tilde\pi$接近。

所以原来的代价函数变成了$L_{\pi}(\tilde{\pi})=\eta(\pi)+\sum_{s} \rho_{\pi}(s) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)$。希望找到新的$\tilde \pi$使得代价函数最大。化成数学形式如下：

$\underset{\theta}{\operatorname{maxmize}}\quad\sum_{s} \rho_{\pi}(s) \sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)\\ s.t. \quad D_{KL}\left(\theta_{\text {old }}, \theta\right) \leq \delta$

但到这里还没结束，还有一个技巧：重要性采样。使得上面这个目标更容易优化。

首先是重要性采样，对于$\sum_{a} \tilde{\pi}(a \mid s) A_{\pi}(s, a)$，直接计算新策略下的期望收益需要重新采样（$ \tilde{\pi}(a \mid s)$是个概率，求和之后是加权平均，也就是期望）。所以就要用重要性采样找到一个简单的分布方便求期望。

用重要性采样的定义，可以写出：

$\sum_{a} \tilde{\pi}\left(a \mid s\right) A_{\pi}\left(s, a\right)=\mathbb{E}_{a \sim \pi}\left[\frac{\tilde{\pi}\left(a \mid s\right)}{\pi\left(a \mid s\right)} A_{\pi}\left(s, a\right)\right]$

所以原式就变成了

$\underset{\theta}{\operatorname{maxmize}}\quad\sum_{s} \rho_{\pi}(s) \mathbb{E}_{a \sim \pi}\left[\frac{\tilde{\pi}\left(a \mid s\right)}{\pi\left(a \mid s\right)} A_{\pi}\left(s, a\right)\right]\\ s.t. \quad D_{KL}\left(\theta_{\text {old }}, \theta\right) \leq \delta$

然后刚才说到：

$\rho_{\pi}(s)=P\left(s_{0}=s|\pi\right)+\gamma P\left(s_{1}=s|\pi\right)+\gamma^{2} P\left(s_{2}=s|\pi\right)+\ldots=\sum_{t = 0}^{\infty} \gamma^{t} P\left(s_{t}=s|\pi\right)$

所以，将$\sum_{s} \rho_{\pi}(s)$写开：

$\sum_{s} \rho_{\pi}(s)=\sum_{s} \sum_{t=0}^{\infty} \gamma^{t} P\left(s_{t}=s \mid \pi\right) .$

然后交换求和顺序

$\sum_{s} \rho_{\pi}(s)=\sum_{t=0}^{\infty} \gamma^{t} \sum_{s} P\left(s_{t}=s \mid \pi\right)$

因为$\sum_{s} P\left(s_{t}=s \mid \pi\right)=1$（概率的归一性），所以$\sum_{s} \rho_{\pi}(s)=\sum_{t=0}^{\infty} \gamma^{t} \cdot 1=\sum_{t=0}^{\infty} \gamma^{t}$，这里的$\sum_{t = 0}^{\infty} \gamma^{t}$是一个几何级数，然后通过无穷级数求和的公式，可以知道，当公比 $|\gamma|<1$ 时，无穷几何级数 $\sum_{t=0}^{\infty} \gamma^{t}$ 收敛，其和为：

$\frac{1}{1-\gamma}$

所以可知$\sum_{s} \rho_{\pi}(s)\cdot(1-\gamma)=1$，所以$\rho_{\pi}(s)\cdot(1-\gamma)$是一个概率。

那么

$\frac{1}{1-\gamma}\sum_{s} \rho_{\pi}(s)\cdot(1-\gamma)\cdot f(s)=\frac{1}{1-\gamma} E_{s \sim \tilde{\rho}_{\pi}}[f(s)]$

所以最后整个式子就可以化成：

$\begin{array}{ll} \underset{\theta}{\operatorname{maxmize}} & \frac{1}{1-\gamma} \mathbb{E}_{s \sim \tilde{\rho}_{\pi},a \sim \pi}\left(\frac{\tilde{\pi}(a \mid s)}{\pi(a \mid s)} A_{\pi}(s, a)\right) \\ \text { subject to } & D_{\mathrm{KL}}\left(\theta_{\text {old }}, \theta\right) \leq \delta \end{array}$

剩下的求解就是最优化范畴了，这里就不写啦，感兴趣的可以自己去探究。

PPO

全称叫Proximal Policy Optimization。

参考：B站视频、可视化

思想

TRPO的问题是KL散度本身就难算，它还在约束条件里，所以就更难了。所以后面就提出了PPO，是对TRPO的优化。一是将约束放在优化目标中，就变成了无约束优化问题。二是将KL散度去掉，改成更容易计算的限制。前者是PPO-penalty，后者是PPO-clip，PPO-clip是对PPO-penalty的优化。

算法

PPO-penalty

PPO-penalty通过将TRPO的约束放在优化目标中，使TRPO变成了一个无约束优化问题。数学形式如下：

$\underset{\theta}{\operatorname{maxmize}} \quad \frac{1}{1-\gamma} \mathbb{E}_{s \sim \tilde{\rho}_{\pi},a \sim \pi}\left(\frac{\tilde{\pi}(a \mid s)}{\pi(a \mid s)} A_{\pi}(s, a)\right)-\beta D_{\mathrm{KL}}\left(\theta_{\text {old }}, \theta\right)$

只是将约束简单的放到了目标函数当中。

PPO-clip

PPO-penalty虽然变成了无约束优化问题，但是还是需要计算KL散度，还是很难算。既然只是要限制$\theta$相对于$\theta_{old}$不要更新太多。PPO-clip采取了一个很简单的方法，就是将$\frac{\tilde{\pi}(a \mid s)}{\pi_{\theta}(a \mid s)}$限制在一个范围内，这样新策略选出来的行为和旧策略选出来的行为就不会差太多。

所以要优化函数的数学形式如下：

$\underset{\theta}{\operatorname{maxmize}} \quad \min \left(\frac{\tilde\pi(a \mid s)}{\pi_{}(a \mid s)} A_{\pi}(s, a), \quad \operatorname{clip}\left(\frac{\tilde\pi(a \mid s)}{\pi_{}(a \mid s)}, 1-\epsilon, 1+\epsilon\right) A_{\pi}(s, a)\right)$

这样新策略$\tilde \pi$选择行为$a$的概率和旧策略$\pi$差太多的时候，新策略就会被限制，避免策略变化的幅度太大。

GRPO

终于到GRPO了。感动

参考视频：B站视频

思想

GRPO算法在DeepSeekMath论文中提出，下面是摘自论文中的图。

在PPO算法中，需要通过计算$V_\pi(s)$来得到优势函数$A(s,a)$的值，而为了计算$V_\pi(s)$，又需要一个神经网络。而GRPO就通过其他方法计算了优势函数$A(s,a)$的值，就不需要用神经网络拟合$V_\pi(s)$了。

算法

还是看论文中的配图，GRPO的策略模型会生成很多个输出$o_1\cdots o_G$，如果是大语言模型，就会生成多个回答。然后通过奖励函数，就可以计算出多个奖励$r_1\cdots r_G$。然后用：

$\hat{A}_{i,t}=\widetilde{r}_{i}=\frac{r_{i}-\operatorname{mean}(\mathbf{r})}{\operatorname{std}(\mathbf{r})}$

这里的$t$代表的是token，因为论文中讲的是大模型

就可以计算出优势函数的值。

最后定义出来的目标函数如下（截自论文）：

$\begin{aligned} \mathcal{J}_{G R P O}(\theta) & =\mathbb{E}\left[q \sim P(Q),\left\{o_{i}\right\}_{i=1}^{G} \sim \pi_{\theta_{o l d}}(O \mid q)\right] \\ & \frac{1}{G} \sum_{i=1}^{G} \frac{1}{\left|o_{i}\right|} \sum_{t=1}^{\left|o_{i}\right|}\left\{\min \left[\frac{\pi_{\theta}\left(o_{i, t} \mid q, o_{i,<t}\right)}{\pi_{\theta_{o l d}}\left(o_{i, t} \mid q, o_{i,<t}\right)} \hat{A}_{i, t}, \operatorname{clip}\left(\frac{\pi_{\theta}\left(o_{i, t} \mid q, o_{i,<t}\right)}{\pi_{\theta_{\text {old }}\left(o_{i, t} \mid q, o_{i,<t}\right)}}, 1-\varepsilon, 1+\varepsilon\right) \hat{A}_{i, t}\right]-\beta \mathbb{D}_{K L}\left[\pi_{\theta}| | \pi_{r e f}\right]\right\} \end{aligned}$

$\min$里面的部分和PPO一样，只不过计算优势函数的方式变了，不再需要神经网络拟合了，然后还加了一项KL散度，论文里说是做一个正则项。